villazoo.blogg.se - Algorithm optimal layout rectangles with overlapping

#ALGORITHM OPTIMAL LAYOUT RECTANGLES WITH OVERLAPPING HOW TO#

For these, the "obvious" method should be optimal: If $A\le12\frac12$, stack $12\frac12\times 20$ rectangles.

where the shortest side is less than $25. The method above neglects "long strips", i.e. Personally I conjecture that even the coverings with loss $\ge1$ are truely optimal in many cases. It does so for all $A\times B$ rectangles with $A\ge25$, $B\ge 25$. In summary, the above method produces a covering that uses at most two rectangles more than an optimal covering as given by the area constraints.

if it was case 3a, the situation is symmetric to above.

If I had a $5 \text\c$ is less than $1$ and hence the covering is optimal. and we show that a discrete and bounded domain convergence analysis is important to get best performance for strong anisotropy. In some cases, the minimum or maximum sizing limitations of the smaller rectangles means I will have to use a few more rectangles. This gives me the minimum amount of rectangles possible, assuming no minimum or maximum sizing limitations. I divide the big rectangle area by the smaller rectangle area. Here's how I manually solve it, takes a while and is messy: Smaller rectangle can't be less than $10$ units in any direction. The intersection divided by the Union gives us the ratio of the overlap to the total area, providing a good estimate of how close the prediction bounding box is. Smaller rectangle can't be more than $20$ units in any direction.

Smaller rectangles can only have a maximum area of $250$ units. I think what I need is an algorithm to do the following,įor any large rectangle, place the least amount of smaller rectangles inside the large rectangle with as equal spacing as possible, the smaller rectangles will all be $A$ units wide and $B$ units long.

#ALGORITHM OPTIMAL LAYOUT RECTANGLES WITH OVERLAPPING HOW TO#

I have a problem I know how to solve by trial and error but I'm trying to figure out the 'smart' way to do it so I can make it into a macro using auto-hotkey and never have to guess and check again. Thus, we can reduce the problem to the one-dimensional problem of determining whether two line segments overlap. This area must be a rectangle where both dimensions are positive, since the boundaries of the intersection are axis aligned. Simulated annealing produced very dense layouts but with an even greater increase in computation time. If the rectangles overlap, they have positive area. Genetic algorithms were better suited to the solution of small to medium sized problems, at the expense of significant computation time. The best result seems to be in this 2014 paper of Brubacher, which gives an algorithm achieving $r\leq 5/2$.Thank God, there is a math section to this site, I'm going insane Meta-heuristic techniques produced good results compared with published algorithms. Start off with an enclosing rectangle that is as high as the highest rectangle, and that has unlimited width. Sort the rectangles by height, greatest height first.

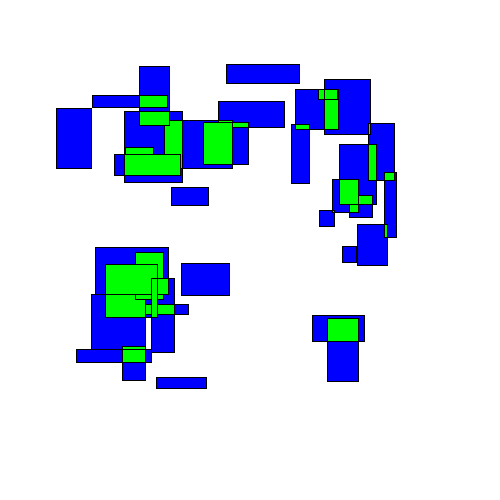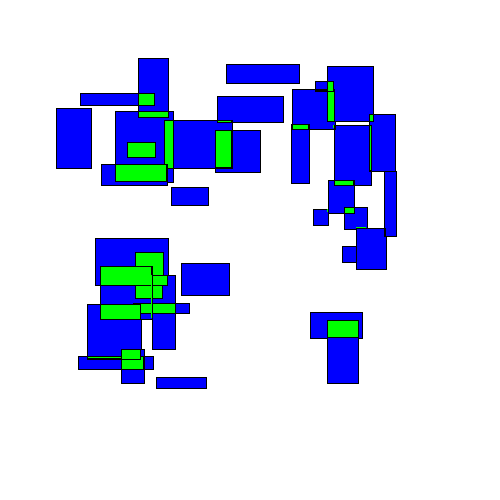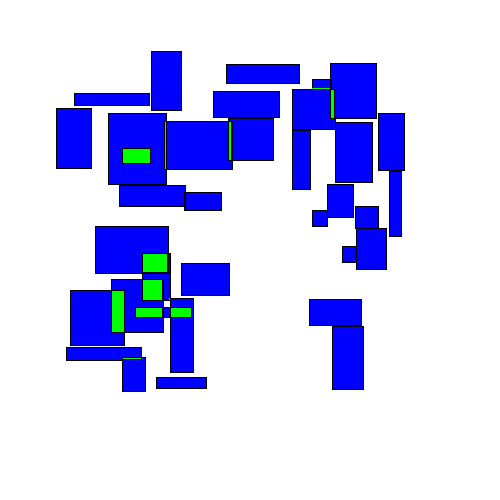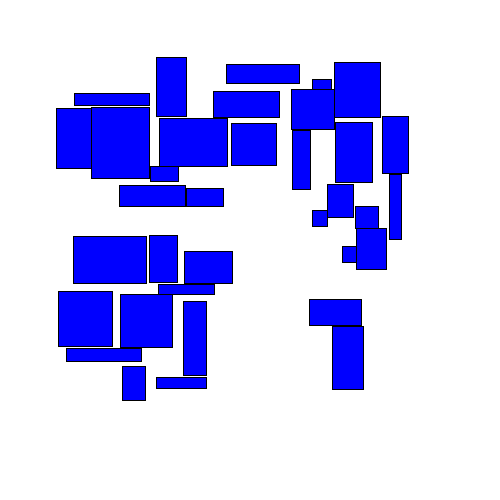
Korf's paper: Optimal Rectangle Packing: Initial Results. There has been some work on the "online" version of this problem where squares are given one at a time and must be packed before the next one is given. The basic algorithm for packing rectangles into an enclosing rectangle of minimum size is described in, for example, Richard E. This paper deals with the effect of exploiting background knowledge for improving an OMR (Optical Music Recognition) deep learning pipeline for transcribing medieval, monophonic, handwritten music from the 12th14th century, whose usage has been neglected in the literature. First, it's easy to see that $r\geq \sqrt$ rectangles (the paper of Meir and Moser discusses this too).įinally, note that the algorithm of Moon and Moser requires knowing the set of squares in advance (since one must sort by their size).